Mathematicians

John Forbes Nash Jr. (1928) works in game theory and differential geometry

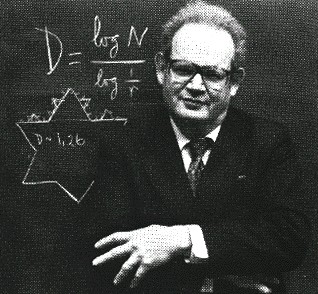
Benoît Mandelbrot (1924)

Raymond Smullyan (1919)

Alfred Horn (1918-2001)

Abraham Robinson (1918-1974)

Edward Norton Lorenz (1917)

Leonard Savage (1917-1971) best known for his book "Foundations of Statistics"

Claude Elwood Shannon (1916-2001)

Yehoshua Bar-Hillel (1915-1975)

Martin Gardner (1914)

Samuel Eilenberg (1913-1998)

Oswald Teichmüller (1913-1943) introduced quasi-conformal mappings

and differential geometric methods into complex analysis

Alan Turing (1912-1954) is the father of modern computer science, because he

invented the Turing machine as well as the Turing Test to determine whether a machine is

conscious and can think, and formulated the "Turing" version of the Church-Turing thesis,

Saunders Mac Lane (1909-2005)

Stephen Cole Kleene (1909-1994)

Saunders MacLane (1909-2005)

Gerhard Gentzen (1909-1945)

Jacques Herbrand (1908-1931)

Kurt Gödel (1906-1978) his most famous works were his incompleteness theorems, the most famous

of which states that any self-consistent recursive axiomatic system powerful enough to describe integer arithmetic

will allow for "true" propositions about integers that can not be proven from the axioms. To prove this theorem,

Gödel developed a technique now known as Gödel numbering, which codes formal expressions into arithmetic

Andrey Kolmogorov (1903-1987)

John von Neumann (1903-1957)

Frank Plumpton Ramsey (1903-1930) developed Ramsey's

theorem which is an important result in combinatorics,

Emil Leon Post (1897-1954)

Wilhelm Ackermann (1896-1962) is most famous for the Ackermann

function named after him, an important example in the theory of computation

Norbert Wiener (1894-1964) cybernetics

Stefan Banach (1892-1945)

Adolf Fraenkel (1891-1965)

George Pólya (1887-1985)

Thoralf Skolem (1887-1963) was a pioneer of mathematicial logic,

Stanislaw Lesniewski (1886-1939) perfected the logical reconstruction of classical mathematics,

Hermann Weyl (1885-1955)

Gaston Maurice Julia (1893-1978)

Luitzen Egbertus Jan Brouwer (1881-1966)

Pierre Joseph Louis Fatou (1878-1929)

Ernst Zermelo (1871-1953)

Hermann Minkowski (1864-1909)

David Hilbert (1862-1943) is most renowned for Hilbert's basis theorem

which solved the principal problem in nineteenth century invariant theory

Giuseppe Peano (1858-1932)

Jules Henri Poincaré (1854-1912) formulated the Poincaré

conjecture and laid the foundations of modern chaos theory

Georg Cantor (1845-1918) created modern set theory

William Kingdon Clifford (1845-1879)

Richard Dedekind (1831-1916) his main contribution to mathematics

is the redefinition of irrational numbers in terms of Dedekind cuts

Chauncey Wright (1830-1875) mathematician and philosopher

Bernhard Riemann (1826-1866) made important contributions to analysis and differential

geometry, some of them paving the way for the later development of general relativity. His name

is connected with the zeta function, the Riemann integral, the Riemann lemma, Riemannian

manifolds, the Riemann mapping theorem, Riemann-Hilbert problems, and Riemann surfaces

Leopold Kronecker (1823-1891)

John Couch Adams (1819-1892) his most famous achievement was

predicting the existence and position of Neptune, using only mathematics

Karl Weierstrass (1815-1897)

George Boole (1815-1864) as the inventor of Boolean algebra, the basis of all modern comuter

arithmetic, he is regarded in hindsight as one of the founders of the field of computer science

Niels Henrik Abel (1802-1829) gave proof of his mathematical genius by

his brilliant solutions of the original problems proposed by Bernt Holmboe

Charles Babbage (1792-1871)

Augustin Louis Cauchy (1789-1857)

Jean François Moufot (1784-1842)

Bernard Bolzano (1781-1848)

Josef Hoëné-Wronski (1778-1853)

Johann Carl Friedrich Gauss (1777-1855) discovered the quadratic reciprocity law, the

prime number theorem and proved several other theorems in algebra as well as number theory

Jan Sniadecki (1756-1830)

Pierre Simon de Laplace (1749-1827) famous for the Laplace

transform, Laplace's equation, and the Laplacian differential operator

Johann Heinrich Lambert (1728-1777)

Maria Gaetana Agnesi (1718-1799) is credited with writing the first book discussing both

differential and integral calculus. When she was 9 years old, she composed and delivered an hour-

long speech in Latin to an academic gathering. The subject was women's right to be educated

Jean le Rond d'Alembert (1717-1783)

Leonard Euler (1707-1783) was the first to use the term "function" (defined by

Leibniz - 1694) to describe an expression involving various arguments; ie: y = F(x).

He is credited with being one of the first to apply calculus to physics

Abraham de Moivre (1667-1754) famous for de Moivre's formula, which links complex

numbers and trigonometry, and for his work on the normal distribution and probability theory

Jakob Bernoulli (1654-1705)

Ehrenfried Walther von Tschirnhaus (1651-1708)

James Gregory (1638-1675)

Blaise Pascal (1623-1662) invented a tabular presentation for binomial coefficients, now called Pascal's triangle

William Brouncker (1620-1684) was the first President of the Royal Society

Pierre de Fermat (1601-1665)

Rene Descartes (1596-1650) invented the Cartesian coordinate system and formulated the basis of

modern geometry (analytic geometry), which in turn influenced the development of modern calculus

Martin Mersenne (1588-1648)

William Oughtred (1575-1660) is credited as the inventor of the slide rule in 1622, and introduced the

"×" symbol for multiplication as well as the abbreviations "sin" and "cos" for the sine and cosine functions

John Napier (1550-1617) is most remembered as the inventor of natural logarithms,

of Napier's bones or Napier's rods and for popularizing the decimal point

Simon Stevin (1548-1620)

François Viète (1540-1603)

Giambattista della Porta (1538-1615) Renaissance cryptographer

Gerolamo Cardano (1501-1576)

Niccolò Fontana Tartaglia (1499-1557)

Adam Riese (1492-1559)

Madhava of Sangamagrama (1350-1425)

Nicolas Oresme (1320-1382)

Thomas Bradwardine (1290-1349)

Gersonides (1288-1344)

Nasir al-Din Tusi (1201-1274)

Leonardo Pisano Fibonacci (1170-1250)

Bhāskara (1114-1185)

Abraham bar Hiyya Ha-Nasi (1070-1136)

Omar Khayyám (1048-1123)

Abul Wafa (940- 998) devised a wall quadrant for the accurate astronomy

measurement of the declination of stars, he also introduced the tangent function

Abu'l-Hasan al-Uqlidisi (fl. 952)

Gerbert of Aurillac (950-1003)

Abu Nasr al Farabi (870-950)

Abu Yusuf (800-870)

Al-Khwarizmi (780-845) is often cited as "the father of algebra", which was named after a part

of the title of his book, Hisab al-jabr w'al-muqabala, along with the algorism number system.

His name is also the root of the word algorithm

Brahmagupta (598-668)

Varahamihira (505-587)

Aryabhata (476-550)

Diophantus (214-298)

Heron of Alexandria (10-70) stated and proved a formula, now known as Heron's formula,

for calculating the area of a triangle in terms of its sides. He also came up with an iterative

process for calculating square roots of numbers

Geminus (110-40 bc)

Theodosius of Bithynia (160-100 bc)

Apollonius of Perga (262-190 bc)

Eratosthenes (276-194 bc) is noted for devising a system of latitude and longitude and computing

the size of the Earth, as well as the Sieve of Eratosthenes as a way of finding prime numbers

Archimedes (287-212 bc)

Nicomedes (280-210 bc) discovered the Conchoid curve

Polyaenus of Lampsacus (3??-278 bc)

Euclid (365-275 bc) the geometrical system outlined in his major work "Elements" is today

referred to as Euclidean geometry to distinguish it from other so-called non-Euclidean

geometries which developed in the 19th century out of investigation into Euclid's fifth

postulate which described the intersection of lines at potentially infinite distances

Arabic numerals (400 bc) were developed in India by the Hindus. Fibonacci promoted the

Arabic numeral system in Europe with his book Liber Abaci, which was published in 1202.

The system did not come into wide use in Europe, however, until the invention of printing

Eudoxus of Cnidus (410-347 bc) was a pupil in mathematics of Archytas in Athens

Archytas (428-347 bc) solved the problem of duplicating the cube in his manner with a

geometric construction, is believed to be the founder of mathematical mechanics

Theodorus of Cyrene (465-398 bc)

Philolaus (480-405 bc) developed Pythagorean number theory

Hippasus (500-4?? bc)

Theano (fl. 6th cent. bc)

Pythagoras (570-480 bc) the Pythagorean theorem states that the sum of the areas of the

squares on the legs of a right triangle is equal to the area of the square on the hypotenuse

Thales (624-547 bc) Thales' theorem states that if A, B and C are points on a circle

where the line AC is a diameter of the circle, then the angle at point B is a right angle